Turinys
Integralas ir jo taikymas
Pirmykštė funkcija
Žymėjimas:
Veiksmo pavadinimas: diferencijavimas arba integravimas.
Funkcija F(x) vadinama funkcijos f(x) pirmykšte funkcija, kai F'(x) = f(x), pvz.:
Kurios funkcijos išvestinė yra funkcija ?
,
C - didžioji!
Neapibrėžtinis integralas
- integralo ženklas.
- pointegralinė funkcija
- integravimo kintamojo diferencialas
- integravimo kintamasis
- pointegralinis reiškinys
- bet koks skaičius (integravimo konstanta)
Integralo skaičiavimo formulės
| Nr. | Funkcija | Funkcijos išvestinė | Pirmykštė funkcija |
|---|---|---|---|
| 1. | | | |
| | | |
|
| | | |
|
| | | |
|
| | | |
|
| | | |
|
| | | |
|
| | | |
|
| 2. | | | |
| 3. | | | |
| | | |
|
| 4. | | | |
| 5. | | | |
| 6. | | | Skaičiuojama pagal kitas taisykles. |
| 7. | | | Skaičiuojama pagal kitas taisykles. |
| 8. | | - | |
| 9. | | - | |
Integralo skaičiavimo taisyklės
- Sudėtinės funkcijos integralo skaičiavimo formulė:
,
- Visada prie gautojo neapibrėžtinio integralo reikia pridėti C!
Apibrėžtinis integralas
Niutono-Leibnico formuuuuuuuuuuuuuuuuuuuulė
Šio reiškinio rezultatas gali būti neigiamas (jei grafikas yra ne pirmame ar antrame ketvirčiuose), todėl reikia:
- naudotis modulio ženklu arba
- pirmiausia apskaičiuoti integralą, po to parašyti plotą.
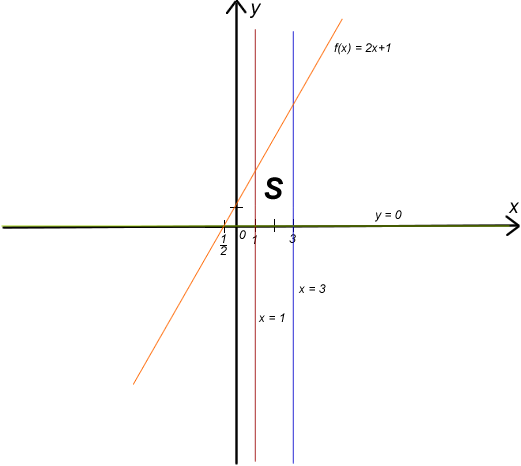
Pavyzdys (kreivinė trapecija)
Vienoje koordinatinėje plokštumoje nubraižykite kreives (tieses):
Apskaičiuokite šiomis kreivėmis apribotos figūros plotą.
(Galima spręsti ir paprasčiau, t.y. be integralų)
Sprendimas (be Integralų)
- Kaip matome, tai yra tiesinė funkcija (f(x)=2x+1), todėl nėra sunku pamatyti, kad tai bus trikampis, kurio plotą galima skaicčiuoti pagal Pitagoro teoremą, o po to pritaikant Herono formulę plotui apskaičiuoti.
- Kadangi turime brėžinį galime, paskaičiuoti kokie yra kraštinių ilgiai arba apskaičiuojant nepasinaudojus grafiko (ištirsime abu atvejus).
- Matome, kad kraštinė ant x ašies riboją šitą figūrą, todėl kraštinės ilgis ant x ašies yra lygus
, o pagal formules skaičiuojame taip :
, o kita koordinatė yra x=3, todėl kraštinės ilgis :
, žiūrime kur susikirs
, matome kad kraštinė prasideda nuo x=0 , todėl
, dabar kai turime dviejų kraštinių ilgius galime sužinoti trečios pagal Pitagoro teoremą :
, O plotas lygus:
ploto vienetai.
- Skaičiuojame, mažojo trikampio kraštines ir plotą, kraštinės skaičiuojame analogiškai didžiąjam trikampiui, todėl : a=1.5, b=3, o
, o
ploto vienetai.
- Beliko vieno trikampio plotą atimti iš kito t.y. :
ploto vienetai.
- Kadangi tai buvo statusis trikampis galima buvo taikyti ploto formulę ,
, bet mano tikslas buvo dar kartu supažindinti ir su Herono formule.