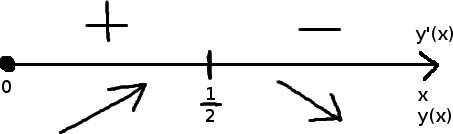Išvestinių taikymas funkcijoms tirti

Duota:

Rasti: didžiausią ir mažiausią funkcijos reikšmes intervaluose:

• a) [-4; 6]
• b) [0; 6]
• c) [-2; 2]

• 
• ,
• 
• ,

Ats.:

Ats.:

Ats.:

Raskite didžiausią funkcijos reikšmę intervale .

• 
• ,
• 
• ,

Ats.:

1. PIRMAS ETAPAS. Matematinio modelio sudarymas
   1. Iš sąlygos nustatyti opimizuojamą dydį, t.y. dydį, kurio mažiausią ar didžiausią reikšmę reikia rasti. Šį dydį pažymėti raide y (arba S, V, R, t, … - priklauso nuo uždavinio sąlygos).
   2. Vieną nežinomą dydį, per kurį palyginus lengva išreikšti optimizuojamą dydį, pavadinti nepriklausomu kintamuoju ir pažymėti x (ar kita raide). Nustatyti x realius rėžius (pagal uždavinio sąlygą).
   3. Pagal uždavinio sąlygą y išreikšti per x. Matematinis modelis bus sudarytas, jei bus surasta funkcija y = f(x). Jos apibrėžimo sritis X yra pagal uždavinio sąlygą galimos nepriklausomos kintamojo reikšmės.
2. ANTRAS ETAPAS. Darbas su matematiniu modeliu
   1. Surasti funkcijos y = f(x), x ∈ X didžiausią ir/arba mažiausią reikšmes (priklauso nuo to, ko reikalauja uždavinio sąlyga).
3. TREČIAS ETAPAS. Atsakymas pagal uždavinio sąlygą
   1. Reikia atsakyti konkrečiai į uždavinio klausimą.

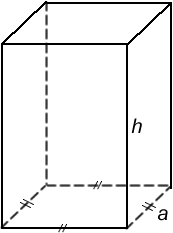
Atviro bako, kurio pagrindas yra kvadratas, tūris - 108 cm². Kokių matmenų bakui pagaminti bus sunaudota mažiausiai medžiagos?

1. Stačiakampio gretasienio paviršiaus plotas turi būti mažiausias.
   • 
2. Stačiakampio gretasienio pagrindo kraštinė a lygi x cm.
   • 
   • 
   • 
   • ,

• ,
• Mažiausia reikšmė:
• 

Ats.: pagrindo kraštinė - 6 cm, aukštis - 3 cm.