Turinys
Laipsninės funkcijos
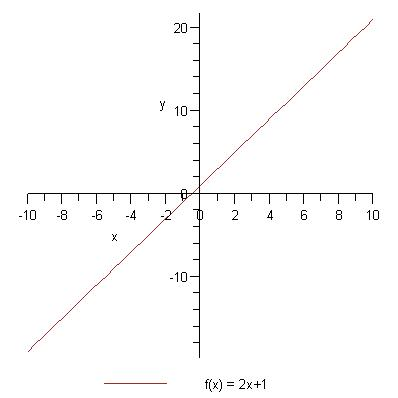
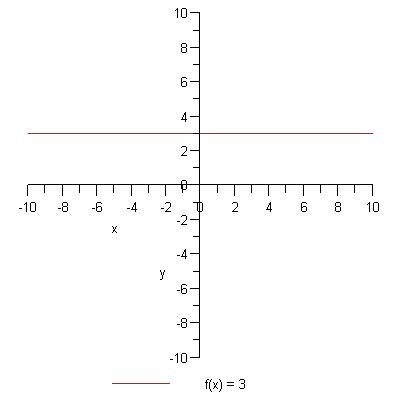
Tiesinė funkcija
arba
Šios funkcijos grafikas - tiesė.
a
Pavyzdys (k != 0)
Pavyzdys (k = 0)
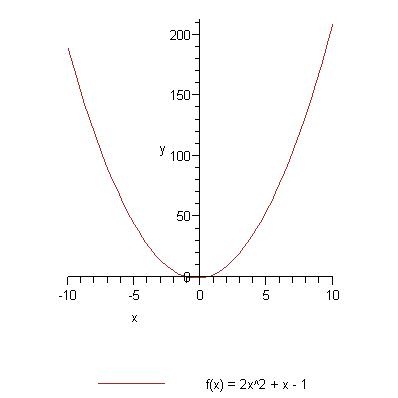
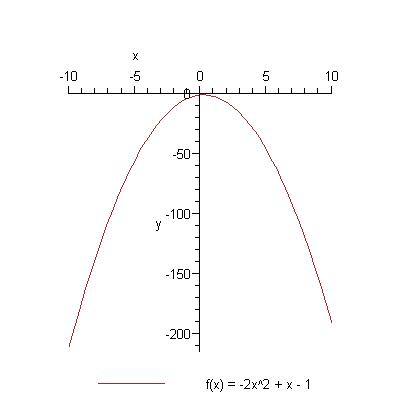
Kvadratinė funkcija
- Jei
, tai
- Jei
, tai
Šios funkcijos grafikas - parabolė.
Pavyzdys (a > 0)
Pavyzdys (a < 0)
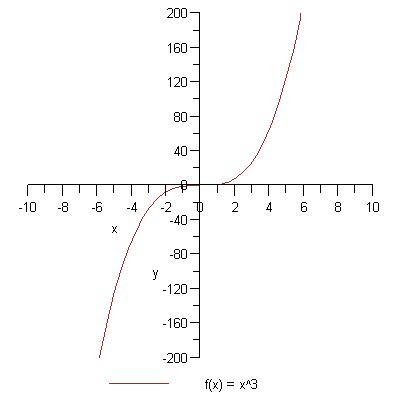
Kubinė funkcija
Šios funkcijos grafikas - kubinė parabolė.
Pavyzdys
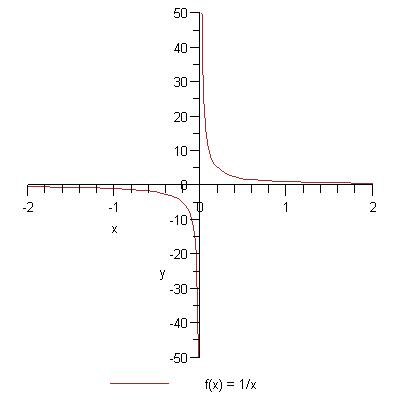
Atvirkštinio proporcingumo funkcija
y = a/x
arba
Šios funkcijos grafikas - hiperbolė.
Pavyzdys
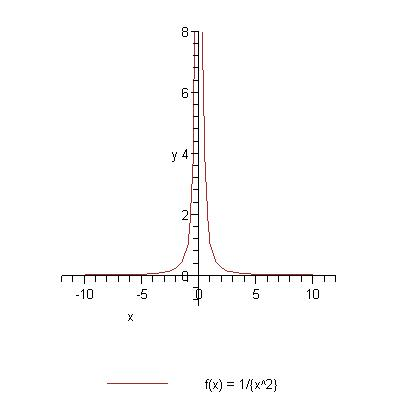
y = a/x^2
Pavyzdys
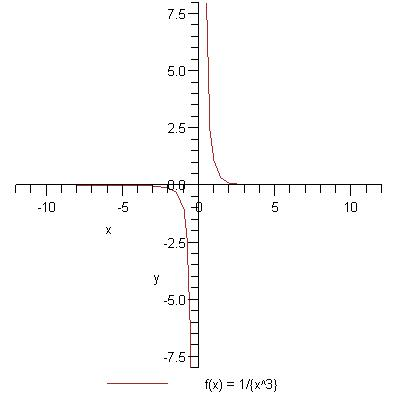
y = a/x^3
Pavyzdys
Šaknys
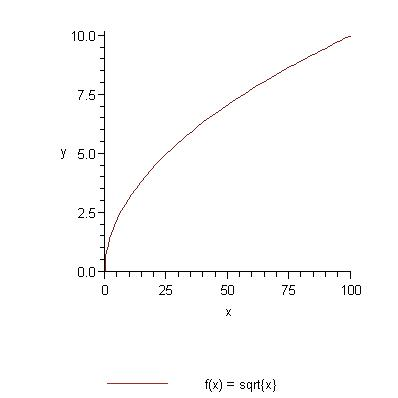
y = sqrt{x}
Pavyzdys
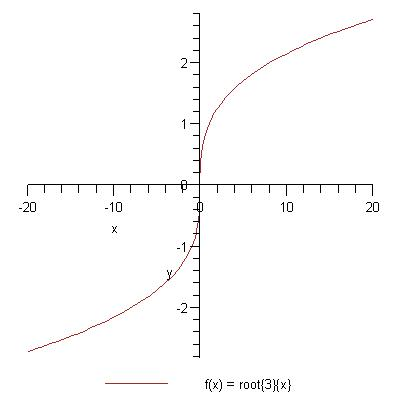
y = root{3}{x}
Pavyzdys
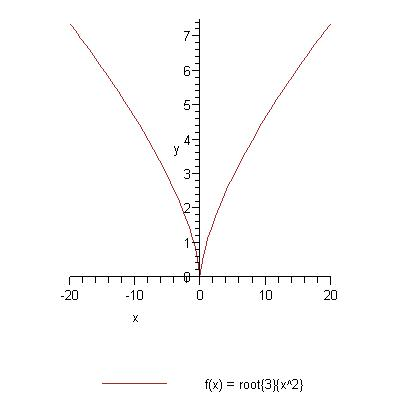
y = root{3}{x^2}
Pavyzdys
Jei nenurodyta kitaip, šio wiki turinys ginamas tokia licencija: CC Attribution-Noncommercial-Share Alike 4.0 International