Turinys
Vektorių algebra
Dar žr. Vektoriai
Vektoriaus daugyba iš skaičiaus
Vektoriaus ir skaičiaus k (
) sandauga vadinamas vektorius, kurio ilgis yra
.
Jeigu , tai naujasis vektorius bus tos pačios krypties kaip ir vektorius
.
Jeigu , tai naujasis vektorius bus priešingos krypties nei vektorius
.
Vektorių sudėtis
Kai vektoriai a ir b nėra kolinearūs
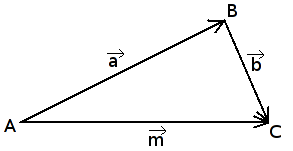
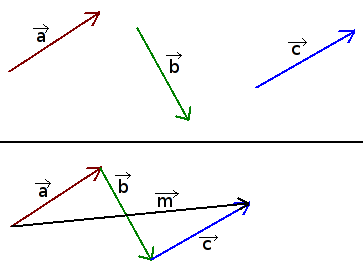
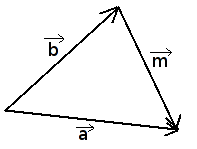
Trikampio taisyklė
Iš vektoriaus pabaigos atidedamas antrasis vektorius
. Vektorius, jungiantis pirmojo vektoriaus
pradžią su antrojo
pabaiga, yra šių vektorių suma.
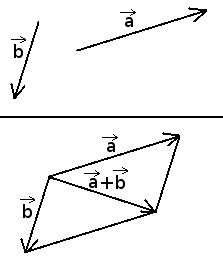
Lygiagretainio taisyklė
Lygiagretainio taisyklė - ir
pradžia yra tas pats taškas. Turimą brėžinį papildome iki lygiagretainio.
ir
suma yra sudaryto lygiagretainio įstrižainė, išvesta iš to paties taško.
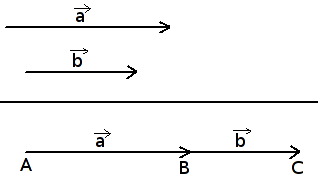
Kai vektoriai yra vienos krypties
Kai vektoriai yra priešpriešiai
Daugiakampio taisyklė
Vektorių suma, lygi nuliniam vektoriui
Vektorių atimtis
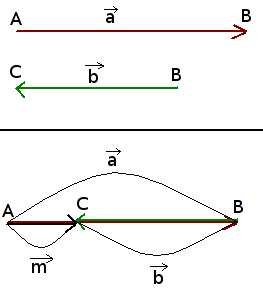
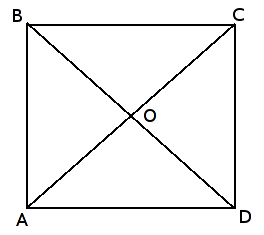
Atimties taisyklė: jei du vektoriai yra atidėti iš vieno taško, tai vektorius, jungiantis antrojo vektoriaus galo tašką su pirmojo galo tašku, lygus pirmojo ir antrojo vektorių skirtumui.
argi?
O paprasčiausia atimtis:
Vieno vektoriaus išreiškimas kitais vektoriais
Vektorių skaliarinė sandauga
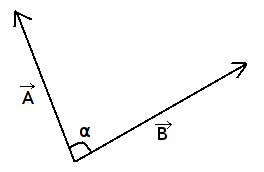
Dviejų nenulinių vektorių skaliarinė sandauga vadinamas skaičius, lygus tų vektorių ilgių ir kampo tarp jų kosinuso sandaugai.
Pavyzdys
Kiti atvejai
- Kai kampas tarp vektorių yra statusis: