Turinys
Funkcijos
Dar žr. Funkcijų grafikai
Funkcija vadinama taisyklė, kuri kiekvienai vieno kintamojo reikšmei priskiria vienintelę kito kintamojo reikšmę. Pirmąjį kintamąjį (x) vadiname funkcijos nepriklausomu kintamuoju (argumentu), o antrąjį (y = f(x)) - priklausomu kintamuoju (reikšme).
Funkcijos y = f(x), kurios apibrėžimo sritis yra X(x; f(x)), kai x ∈ .
X
Apibrėžimo ir reikšmių sritys
Aibę tų reikšmių, kurias gali įgyti nepriklausomas kintamasis x, vadiname funkcijos apibrėžimo sritimi ir žymime D(f).
Aibę tų reikšmių, kurias įgyja priklausomas kintamasis y, vadiname funkcijos reikšmių sritimi ir žymime E(f).
Laipsninė funkcija
Dar žr. Funkcijų grafikai -> Laipsninės funkcijos
Funkcija, kurią galima išreikšti formule f(x) = xp (x - kintamasis, p - skaičius), vadiname laipsnine funkcija.
Rodiklinė funkcija
Dar žr. Funkcijų grafikai -> Rodiklinės funkcijos
Funkcija, kurią galima užrašyti formule f(x) = ax (a > 0, a ≠ 1), vadinama rodikline funkcija.
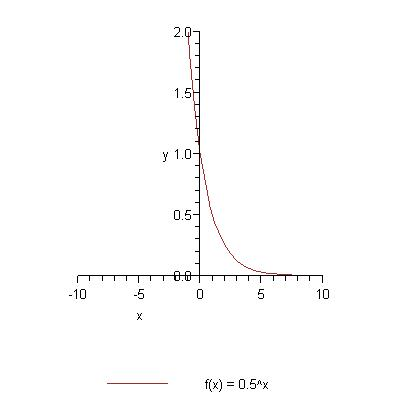
Kai 0 < a < 1
| x | -3 | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|---|
| y | 8 | 4 | 2 | 1 | 0.5 | 0.25 |
D(y) = (-∞; ∞)
E(y) = (0; ∞)
Nei lyginė, nei nelyginė.
Mažėjanti.
Didžiausios/mažiausios reikšmės nėra.
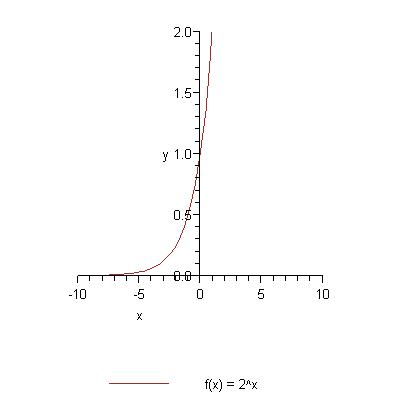
Kai 0 < a < 1
| x | -2 | -2 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|
| y | 0.25 | 0.5 | 1 | 2 | 4 | 8 |
D(y) = (-∞; ∞)
E(y) = (0; ∞)
Nei lyginė, nei nelyginė.
Didėjanti.
Didžiausios/mažiausios reikšmės nėra.
Rodiklinės lygtys
 turbūt ne čia.
turbūt ne čia.
Rodikline lygtimi vadinama lygtis, kurios kintamasis yra laipsnių rodiklyje.
Sprendimo būdai:
- grafinis;
- suvedant prie vienodo laipsnio pagrindo;
- iškeliant prieš skliaustus bendrą dauginamąjį su kintamuoju;
- naudojant keitinį;
- dalijant iš to paties reiškinio.
Bendro dauginamojo su nežinomuoju kėlimas prieš skliaustus
1-as būdas
,
2-as būdas
,
Rodiklinės lygties suvedimas į kvadratinę įvedant naują kintamąjį
1-as pavyzdys
,
,
,
Ats.: 0; 1.
2-as pavyzdys
|
- …
,
,
, x=-2.
Ats.: 2.
Rodiklinės lygties narių dalijimas iš to paties reiškinio (homogeninės lygtys)
|
- …
Ats.: 0.