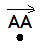Turinys
Vektoriai
Dar žr. Vektorių algebra
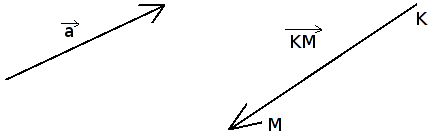
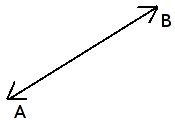
Vektorius - kryptinė atkarpa.
Žymėjimas
Vektoriaus ilgis
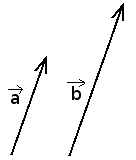
Lygūs vektoriai
Vektoriai, kurių ilgis yra vienodas, o kryptys sutampa, vadinami lygiais vektoriais.
,
,
(skiriasi kryptys),
(skiriasi kryptys)
Nulinis vektorius
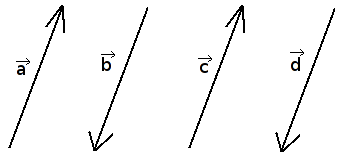
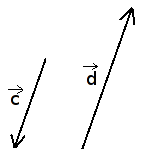
Kolinearūs vektoriai
Nenuliniai vektoriai, esantys vienoje tiesėje arba lygiagrečiose tiesėse, vadinami kolineariaisiais.
Kolinearių vektorių rūšys: vienos krypties, priešpriešiai.
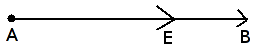
Vienos krypties
Priešpriešiai
Vienakrypčiai
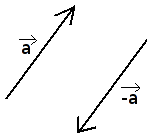
Priešingi vektoriai
(
) priešinguoju vektoriumi vadinamas to paties ilgio priešpriešinis vektorius.
Pavyzdys 1
Pavyzdys 2
Vienetinis vektorius (ortas)
Vektorius, kurio ilgis lygus 1, vadinamas vienetiniu.
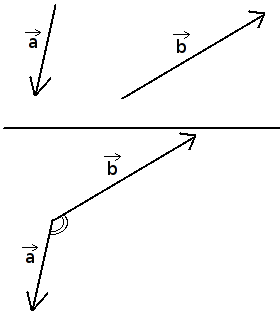
Kampas tarp dviejų vektorių
Jei nenurodyta kitaip, šio wiki turinys ginamas tokia licencija: CC Attribution-Noncommercial-Share Alike 4.0 International